ТЕОРИЯ ГРАФОВ

Практикум

по дисциплине «Дискретная математика»

1. Краткий перечень основных понятий теории графов

1.1. Общие понятия

Графы помогают описывать и исследовать различные системы объектов и их связи. Например, в графе, изображенном на рис. 1, точки (вершины графа) можно интерпретировать как города, а линии, соединяющие вершины (ребра), как дороги, соединяющие эти города.

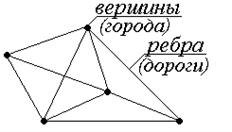
Рис. 1.

Формальное определение графа таково [1-8]. Графом Г=(V,X) называется пара множеств: V – множество, элементы которого называются вершинами, X – множество неупорядоченных пар вершин, называемых ребрами. Если v, w Î V, x=(v,w)ÎX, то говорят, что ребро x соединяет вершины v и w или x инцидентно v и w. Таким образом, {v,w} – обозначение ребра. Если Х представляет собой упорядоченные пары (т. Е. X – подмножество декартова произведения V×V), то граф называется ориентированным, а пары {v,w} называют дугами. Если множеству X принадлежат пары v=w, то такие ребра (v,v) называют петлями. Существование одинаковых пар {v,w} соответствует наличию параллельных или кратных ребер (дуг), а кратностью ребер называют количество таких одинаковых пар.

Например, кратность ребра {v₁, v₂} в графе, изображенном на рис. 2, равна двум, кратность ребра {v₃, v₄} − трем.

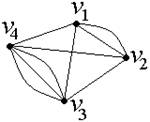
Рис.2.

Псевдограф − граф, в котором есть петли и/или кратные ребра.

Мультиграф − псевдограф без петель.

Заметим, что графом также называют мультиграф, в котором ни одна пара не встречается более одного раза.

Итак, используемые далее обозначения:

V – множество вершин;

X – множество ребер или дуг;

v (или v_i)– вершина или номер вершины;

G, G₀ – неориентированный граф;

D, D₀ – ориентированный;

{v,w} − ребра неориентированного графа;

{v,v} – обозначение петли;

(v,w) − дуги в ориентированном графе;

v,w – вершины, x,y,z – дуги и ребра;

n(G), n(D) количество вершин графа;

m(G) – количество ребер, m(D) – количество дуг.

Примеры

1) Ориентированный граф D=(V, X), V={v₁, v₂, v₃, v₄},

X={x₁=(v₁,v₂), x₂=(v₁,v₂), x₃=(v₂,v₂), x₄=(v₂,v₃)}.

Рис. 3.

2) Неориентированный граф, изображенный на рис. 4:

G=(V, X), V={v₁, v₂, v₃, v₄, v₅},

X={x₁={v₁,v₂}, x₂={v₂,v₃}, x₃={v₂,v₄}, x₄={v₃,v₄}}.

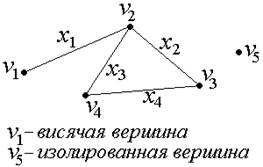
Рис. 4.

1.2. Понятия смежности, инцидентности, степени

Если x={v,w} - ребро, то v и w − концы ребра x.

Если x=(v,w) - дуга ориентированного графа, то v − начало, w – конец дуги.

Вершина v и ребро x неориентированного графа (дуга x ориентированного графа) называются инцидентными, если v является концом ребра x (началом или концом дуги x ).

Вершины v, w называются смежными, если {v,w}ÎX.

Степенью вершины v графа G называется число d(v) ребер графа G, инцидентных вершине v.

Вершина графа, имеющая степень 0 называется изолированной, а степень 1 – висячей.

Полустепенью исхода (захода) вершины v ориентированного графа D называется число d⁺(v) (d^-(v)) дуг ориентированного графа D, исходящих из v (заходящих в v).

Следует заметить, что в случае ориентированного псевдографа вклад каждой петли инцидентной вершине v равен 1 как в d⁺(v), так и в d^-(v).

1.3. Маршруты и пути

Последовательность v₁x₁v₂x₂v₃…x_kv_k₊₁, (где k³1, v_iÎV, i=1,…,k+1, x_iÎX, j=1,…,k), в которой чередуются вершины и ребра (дуги) и для каждого j=1,…,k ребро (дуга) x_j имеет вид {v_j,v_j₊₁} (для ориентированного графа (v_j,v_j₊₁)), называется маршрутом, соединяющим вершины v₁ и v_k₊₁ (путем из v₁ в v_k₊₁).

Пример

В графе, изображенном на рис.4, v₁x₁v₂x₂v₃x₄v₄x₃v₂ – маршрут, v₂x₂v₃x₄v₄ – подмаршрут;

маршрут можно восстановить и по такой записи x₁x₂x₄x₃ ;

если кратности ребер (дуг) равны 1, можно записать и так v₁v₂v₃v₄v₂ .

Цепь − незамкнутый маршрут (путь), в котором все ребра (дуги) попарно различны.

Цикл − замкнутая цепь (в неориентированном графе).

Контур − замкнутый путь (в ориентированном графе).

Простой путь (цепь) − путь (цепь, цикл, контур), в котором ни одна дуга/ребро не встречается дважды.

Простой цикл (контур) − цикл (контур), в котором все вершины попарно различны.

Гамильтонова цепь (путь, цикл, контур) − простая цепь (путь, цикл, контур), проходящая через все вершины.

Эйлерова цепь (путь, цикл, контур) − цепь (путь, цикл, контур), содержащая все ребра (дуги) графа по одному разу.

Длина маршрута (пути) − число ребер в маршруте (дуг в пути).

Утверждение 1. Для того чтобы связный псевдограф G обладал Эйлеровым циклом, необходимо и достаточно, чтобы степени всех его вершин были четными.

Утверждение 2. Для того чтобы связный псевдограф G обладал Эйлеровой цепью, необходимо и достаточно, чтобы он имел ровно 2 вершины нечетной степени.

1.4. Матрицы смежности и инцидентности

Пусть D=(V,X) ориентированный граф, V={v₁,...,v_n}, X={x₁,...,x_m}.

Матрица смежности ориентированного графа D − квадратная матрица

A(D)=[a_ij] порядка n, где

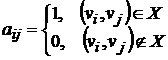
Матрица инцидентности − матрица B(D)=[b_ij] порядка n´m, где

Матрицей смежности неориентированного графа G=(V,X) называется квадратная симметричная матрица A(G)=[a_ij] порядка n, где

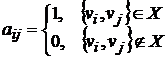Для ориентированного графа

Матрицей инцидентности графа G называется матрица B(G)=[b_ij] порядка n´m, где

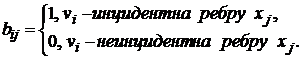
1.5. Связность. Компоненты связности

Подграфом графа G (ориентированного графа D) называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G (D).

Подграф называется собственным, если он отличен от самого графа.

Говорят, что вершина w ориентированного графа D (графа G) достижима из вершины v, если либо w=v, либо существует путь (маршрут) из v в w.

Граф (ориентированный граф) называется связным (сильно связным), если для любых двух его вершин v, w существует маршрут (путь), соединяющий v и w.

Компонентой связности графа G (сильной связности ориентированного графа D) называется его связный (сильно связный) подграф, не являющийся собственным подграфом никакого другого связного (сильно связного) подграфа графа G (ориентированного графа D).

1.6. Матрицы достижимости и связности

Пусть A(D) – матрица смежности ориентированного псевдографа D=(V,X) (или псевдографа G=(V,X)), где V={v₁,…, v_n}. Обозначим через A^k=[a⁽^k⁾_ij] k-ю степень матрицы смежности A(D).

Элемент a⁽^k⁾_ij матрицы A^k ориентированного псевдографа D=(V,X) (псевдографа G=(V,X)) равен числу всех путей (маршрутов) длины k из v_i в v_j.

Матрица достижимости ориентированного графа D − квадратная матрица T(D)=[t_ij] порядка n, элементы которой равны

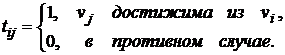
Матрица сильной связности ориентированного графа D − квадратная матрица S(D)=[s_ij] порядка n, элементы которой равны

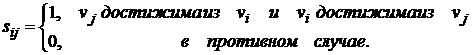
Матрица связности графа G − квадратная матрица S(G)=[s_ij] порядка n, элементы которой равны

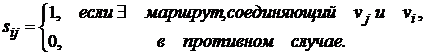
Утверждение 3. Пусть D=(V,X) – ориентированный граф, V={v₁,…, v_n}, A(D) – его матрица смежности. Тогда

1) T(D)=sign[E+A+A²+A³+… A^n-1],

2) S(D)=T(D)&T^T(D) (T^T-транспонированная матрица, &- поэлементное умножение).

Пусть G=(V,X) – граф, V={v₁,…, v_n}, A(G) – его матрица смежности. Тогда

S(G)=sign[E+A+A²+A³+… A^n-1] (E- единичная матрица порядка n).

1.7. Расстояния в графе

Пусть - граф (или псевдограф). Расстоянием между вершинами называется минимальная длина пути между ними, при этом , , если не пути.

Расстояние в графе удовлетворяют аксиомам метрики

1) ,

2) (в неориентированном графе)

4) в связном неориентированном графе.

Пусть связный граф (или псевдограф).

Диаметром графа G называется величина .

Пусть .

Максимальным удалением (эксцентриситетом) в графе G от вершины называется величина .

Радиусом графа G называется величина

Центром графа G называется любая вершина такая, что .

1.8. Образ и прообраз вершины и множества вершин

Пусть ориентированный граф - некоторая вершина .

Обозначим - образ вершины ;

- прообраз вершины ;

- образ множества вершин V₁ ;

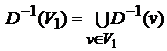- прообраз множества вершин V₁.

1.9. Нагруженные графы

Нагруженный граф − ориентированный граф D=(V,X), на множестве дуг которого определена некоторая функция , которую называют весовой функцией.

Цифра над дугой (см. рис. 5)− вес дуги (цена дуги).

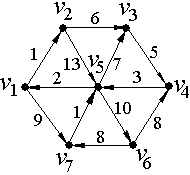
Рис. 5.

Обозначения: для любого пути П нагруженного ориентированного графа D через l(П) сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько она входит в путь П).

Величина l называется длиной пути.

Если выбрать веса равными 1, то придем к ненагруженному графу.

Путь в нагруженном ориентированном графе из вершины v в вершину w, где v¹w, называется минимальным, если он имеет наименьшую длину.

Аналогично определяется минимальный путь в нагруженном графе.

Введем матрицу длин дуг C(D)=[c_ij] порядка n, причем

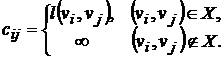
Свойства минимальных путей в нагруженном ориентированном графе

1) Если для " дуги , то " минимальный путь (маршрут) является простой цепью;

2) если минимальный путь (маршрут) то для " i,j : путь (маршрут) тоже является минимальным;

3) если − минимальный путь (маршрут) среди путей (маршрутов) из v в w, содержащих не более k+1 дуг (ребер), то − минимальный путь (маршрут) из v в u среди путей (маршрутов), содержащих не более k дуг (ребер).

1.10. Деревья и циклы

Граф G называется деревом если он является связным и не имеет циклов.

Граф G называется лесом если все его компоненты связности - деревья.

Свойства деревьев:

Следующие утверждения эквивалентны:

1) Граф G есть дерево.

2) Граф G является связным и число его ребер ровно на 1 меньше числа вершин.

3) " две различные вершины графа G можно соединить единственной (и при этом простой) цепью.

4) Граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один и притом простой цикл

Утверждение 4. Если у дерева G имеется, по крайней мере, 1 ребро, то у него найдется висячая вершина.

Утверждение 5.Пусть G связный граф, а − висячая вершина в G, граф получается из G в результате удаления вершины и инцидентного ей ребра. Тогда тоже является связным.

Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Пусть G – связный граф. Тогда остовное дерево графа G должно содержать n(G)-1 ребер. Значит, для получения остовного дерева из графа G нужно удалить ребер.

Число называется цикломатическим числом графа G.